1802년, 케임브리지 대학이 낸 수학문제

오늘은 1802년, 영국의 어느 대학에서 출제한 수학문제를 풀어보자.

보기만 해도 머리가 아파오지만,

1. 일단은 무한수의 합이 얼마인지에 대한 문제.

2. 분모가 1x2, 2x3, 3x4, ... 즉 (n * (n+1)) 식의 패턴을 가지고 있다는 것 까지는 알 수 있을 것 같다.

...

아래 해결방법을 보기 전에, 어떻게 해결해야 할지, 깊게 숨을 한 번 내쉬어 보고, 더불어 아래의 광고도 한 번 보면서, 해결 방법에 대해 조금 생각해 보는 시간을 가져보자.

준비 되었으면,

1. 앞에서 이야기한 바와 같이, 분모가 [n(n + 1)]이므로 식을 단순화 하면, 1/[n(n + 1)]

2. 이 문제의 트릭은 분모가 두개의 조건, n 과 n+1의 곱을 가지고 있다는 것이다. 이것은 (n+1)과 (n)을 가진 두개의 분모의 합으로 표현할 수 있다. (이것을 부분분수분해(Partial fraction decomposition)라고 함) 그래서 1번의 단순화 형식을 아래와 같이 나타낼 수 있다.

1/[n(n + 1)] = A/n + B/(n + 1)

3. 양변에 [n(n + 1)]을 곱하면, 1 = A(n + 1) + B(n)

이것은 다시,

1 = An + A + Bn

1 = A + n(A + B)

n의 값에 관계없이 좌우 값이 일치하기 위해서는 n(A+B)가 0 이 되어야 하고, 이 경우 A는 1이다.

A가 1인 경우 B는 –1, 즉

A = 1

A + B = 0

1 + B = 0

B = -1

이제 A, B의 값을 찾았으니, 위의 2번 식에 대입해 보면,

1/[n(n + 1)] = 1/n – 1/(n + 1)

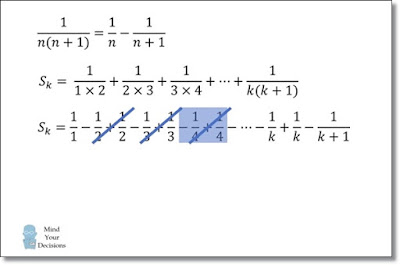
이것을 이용하면 아래와 같이 문제를 더 단순화 할 수 있다.

1/(1×2) = 1/1 – 1/2

1/(2×3) = 1/2 – 1/3

1/(3×4) = 1/3 – 1/4

…

이제 남는 것은,

Sk = 1 – 1/(k + 1)

k가 무한대로 수렴할 때, – 1/(k + 1) = 0

그러므로,

1/(1×2) + 1/(2×3) + 1/(3×4) + … = 1 !!!

학위를 받기 위해 이런 문제를 풀어야 했던 1802년도 케임브리지 대학생들에게 경의를 보낸다.

...

그럼 우리나라는, 1802년 우리나라에는 어떤 일이 있었을까? 궁금했다. 

1802년, 영,정조시대가 끝나고 즉위한 순조. 그 순조2년이 바로 1802년.

안동김씨의 세도정치가 시작된 해. 그로 인해 피폐해진 민심에 1811년, 홍경래의 난이 발생하는 등 이후 60년 동안 외척들로 인해 나라와 백성의 삶이 어려워지기 시작한 원년이 1802년.

서양의 학생들이 고등수학의 해법을 고민하던 때, 우리나라는 왕의 친족이라는 이유만으로 백성의 등골을 빼먹는 자들의 지배가 시작되는 해, 1802년....... 흠.

(알림) 블로그에 올린 글들은 Presh Talwalkar의 유투브 영상과 그의 블로그에서 가져온 것임을 밝힙니다. Presh Talwalkar의 블로그는 여기로 가시면 볼 수 있습니다. 참고로 그의 블로그에는 위 문제가 실린 케임브리지 대학의 출판물 인쇄본 링크외에도 수학과 관련된  좋은 정보도 많이 있습니다. 관심있는 분들은 필히 방문!