뿌듯한 하루, 그리고...

너무 감격적인 하루,

그리고 이제 나만 잘 하면 되겠다는 생각.

달팽이 - PANIC

어느 새 훌쩍 들어 버린 나이에도, 처음 들었을 때의 그때 그 느낌이 고스란히 남아있는, 노래.

 <달팽이, 1995년, 패닉>

집에 오는 길은 때론 너무 길어 나는 더욱더 지치곤 해

문을 열자마자 잠이 들었다가 깨면 아무도 없어

좁은 욕조 속에 몸을 뉘었을 때 작은 달팽이 한 마리가

내게로 다가와 작은 목소리로 속삭여줬어

언젠가 먼 훗날에 저 넓고 거친

세상 끝 바다로 갈 거라고

아무도 못봤지만 기억 속 어딘가

들리는 파도소리 따라서

나는 영원히 갈래

모두 어딘가로 차를 달리는 길 나는 모퉁이 가게에서

담배 한 개비와 녹는 아이스크림 들고 길로 나섰어

해는 높이 떠서 나를 찌르는데 작은 달팽이 한마리가

어느새 다가와 내게 인사하고 노랠 흥얼거렸어

언젠가 먼 훗날에 저 넓고 거칠은

세상 끝 바다로 갈거라고

아무도 못봤지만 기억 속 어딘가

들리는 파도소리 따라서

나는 영원히 갈래

내 모든 걸 바쳤지만 이젠 모두 푸른 연기처럼

산산이 흩어지고

내게 남아 있는 작은 힘을 다해 마지막 꿈속에서

모두 잊게 모두 잊게 해줄 바다를 건널거야

언젠가 먼 훗날에 저 넓고 거친

세상 끝 바다로 갈거라고

아무도 못 봤지만 기억 속 어딘가

들리는 파도소리 따라서

나는 영원히 갈래 

"...문을 열자마자 잠이 들었다가 깨면 아무도 없어. 좁은 욕조 속에 몸을 뉘었을때 작은 달팽이 한 마리가, 내게로 다가와 작은 목소리로 속삭여줬어 ... "

부드러운 피아노 소리와 (누구나 한 번은 느껴 보았을 경험에서 우러나온) 아름다운 가사가 조화로운, 정말 좋은 음악. 지금 다시 들어도 참 좋다.

...


아래는 PANIC의 3집에 실린 음악.

<내 낡은 서랍 속의 바다, 1998년, Sea Within>

Listening music at night

살다보면 뜻하지 않게 실망도 하고, 짜증도 나는 날이 있기 마련. 내가 의도하지 않은 일에 휘말려 하루가 힘들고 약간의 우울함도 밀려 올 때, 그때 들으면 쬐끔 맘이 풀어지는 음악들이 있다.

기타도 잘 치고, 노래도 잘 부르는 처자 – Laura Cox가 부른 Sweet Home Alabama.

이 뮤직비디오를 보고 있으면 오른쪽 입 꼬리가 반쯤은 올라가 있을 것이다. 아니라고? 그렇다면 다음 곡 들어간다.

직접 두들기지 않아도, 신난 표정으로 드럼을 두들기는 것을 보는 것만으로도 절반쯤 맘의 독기가 빠져 나가는 것 같다. 아니라고? 그렇다면....

이 영상에 붙은 Best comment가 재미있다.

“Vocals didn‘t do it for me but the Guitars and Drums made me cum.”

마음속에 오늘의 앙금이 아직 남아 있다면, 신나는 음악과 함께, 위의 커멘트처럼 컴아웃 해 버리자. 그리고 혹시 아는가? - 내일은 일등 복권에 당첨되는 행운이 당신을 기다리고 있을지도........

위잉위잉 - 혁오

가져보지 못한 자는 잃어버리는 슬픔을 알지 못한다고, 상실의 시대를 거쳐 여기까지 왔다면서 잃어버린 것들을 당신 세대는 이야기하지만, 가져보지도 못한 것을 놓을 수는 없다고 눈물을 흘리는 아들.

      “비틀비틀 걸어가는 나의 다리

      오늘도 의미없는 또 하루가 흘러가죠

      사랑도 끼리끼리 하는거라 믿는 나는

      좀처럼 두근두근 거릴일이 전혀없죠“

그래서 그렇게 이야기 할 수도 있겠다. 나는 어떻게든 잘 될 것이라는 마지막 긍정은 놓치지 않으려고 하지만 그것을 아이들에게는 잘 전달하지는 못했나 보다.

그래도 어쩌면, 이런 세상에서 그런 푸르고 푸른 하늘(blue sky)의 기분을 가슴에 단 한순간도 담아보지 못한 사람이 더 불쌍한 것은 아니냐고, 어쩌면 네가 느끼는 지금의 그 파란 기분이, 그런 생각도 한 번 해보지 못한 사람은 가질 수 없는, 나이 들어 식어가는 네 감정에 온기를 불어넣을 수도 있다고.

오늘은 Black(Hole) Friday.

오늘은 블랙(홀) 프라이 데이.

나사에서는 블랙홀 사진을 감상하는, 블랙홀 기념의 날, 이라고......

<In this artist's illustration, turbulent winds of gas swirl around a black hole. Some of the gas is spiraling inward toward the black hole, but another part is blown away.>

<A black hole is a place in space where gravity pulls so much that even light cannot get out. The gravity is so strong because matter has been squeezed into a tiny space.>

<How big are black holes? Black holes can be big or small…just like the lines in all of the stores today. >


지갑의 현금이 블랙홀에 삼켜진 것처럼 사라지는 날 - 블랙 프라이데이, 아니 블랙홀 프라이데이.

ABKO HACKER K935P KEYBOARD

키보드 뒤판을 보니 ‘ABKO HACKER K935P’ 라고 표기되어 있고, 인터넷에서 검색한 모델명은 ‘ABKO HACKER K935P V2 PBT 무접점 텐키리스 (화이트, 45G)’.

하지만 실제 제조사와 모델명은 NIZ EC87-S, 즉 NIZ라는 회사에서 만든 EC87-S 모델명을 가진 키보드를 앱코라는 국내 회사에서 수입하여 모델명만 바꿔 판매중인 듯 – NIZ에서는 검은 색 모델도 있는데, 키캡 재질이 POM으로 되어 있고, 키 압력을 35G로 줄인 제품도 판매중이다. 이 검은 색 모델(NIZ-EC87)는 유튜브에 리뷰도 많다.

<EC – 즉 정전용량(Electrostatic Capacitive)키보드>

출시하자마자 특가로 구매했으니, 구입한 지는 좀 되었다. 일단

장점부터 이야기 하자면,

1) 키캡

개인적으로 키보드를 고를 때는 키캡부터 먼저 확인하는 편인데, 왜냐하면 키캡 잘 만드는 회사가 키보드도 전반적으로 잘 만들기 때문이다. 그런 의미에서 보자면, 이 키보드 키캡 - 잘 만들었다. PBT재질의 레이저로 글쇠표면을 지진 방식인데, 인쇄도 진하게 잘 되었고 폰트도 예쁜 것으로 골라서 새겨 넣은 듯 꽤 좋다. 글쇠 표면은 이쪽이 부드러운 편으로, 키캡 잘 만들기로 소문난 레오폴드의 그 까끌한 표면과 비교해도 이쪽도 감촉이 나쁘지 않다. 손에 땀이 많이 차는 체질인데 손가락에 수분이 많을 때에는 까끌한 것보다는 부드러운 이쪽이 더 두들기기가 좋았다.

2) 키감(두들김)

나쁘지 않다. 이 정전용량 방식 키보드의 원조인 토프레사의 키보드 느낌을 약 80%살렸다고 광고하는데, 그 말에 전적으로 동의한다. 그만큼 두들길 때의 느낌은 리얼포스와 유사하다. 그렇다면, 나머지 20%의 차이점은? 개인적인 생각으로는 이 키보드 혹은 스위치 제조사가 실력이나 특허침해 문제 때문에 나머지 20%를 넣지 못했다는 생각은 들지 않는다. 왜냐하면,

<OEM높이의 키캡을 올리면 리얼포스와 유사한 소리가 난다>

사진과 같이 높이가 좀 높은 OEM Profile, 그리고 두께가 앏은 키캡을 키보드에 올리면 리얼포스와 유사한 소리가 난다. 그렇다면 왜 이 제품엔 두껍고 낮은 체리프로파일 키캡을 올렸을까?

제품 출시시 표시한 광고문구에 힌트가 들어 있다 – 게임용 키보드. 낮은 높이의 키캡을 사용해서 입력시간을 단축하려고 한 흔적이 있다는 것. 그리고 키보드 내부에 들어 있는 실리콘, 즉 멤브레인 고무도 구분감(Tactile)이 거의 없다시피 하는데, 이 부분도 리얼포스의 그 뚜렷한 구분감과 비교가 되는 부분 - 좀 아쉽지만 이 키보드가 지향하는 바는 게임용으로 구분감등으로 빠른 입력에 방해가 되는 부분은 하나씩 제가한 듯싶다. 게다가 슬라이더 쪽에 고무링(아래 사진)을 넣어 소음도 최소화 했다.

(이정도면, 집에서 부모님 몰래 조용히 게임하는 청소년을 위한 키보드라는 표현도 무색하지 않을 듯.)

그럼 단점은?

1) 비키 타입(VIKI type)

왜? 왜? 상판이 없는 이 형식은 정말, 정말 싫다. 스위치를 덮어주는 상판이 없다시피 하는 이런 형식의 키보드는 장점보다는 단점이 많은데, 1) 먼지가 잘 쌓인다. 스위치가 노출된 형식이다보니 스위치 주변에 먼지도 많이 끼고 그 허연 먼지가 잘 보이기도 한다. - 그래서 청소용 솔을 부속품으로 넣어 준 듯.

비키 타입의 장점은, 개인적으로는, 키보드 좌우상하의 여백을 잘라내서 키보드 크기를 극단적으로 줄여보겠다는 시도가 있을 때에나 멋져 보이는 것. 예를 들어 볼텍스 시리즈 키보드 들이 그렇다.

<여백을 과감하게 잘라내어 그 크기를 극도로 줄이겠다는 시도의 좋은 예>

비키타입 키보드의 또하나의 단점은 2) 키캡이 잘 빠지고, 아이들 특히 집에 있는 유아들이 빼서 집어 삼킬 수도 있다. 집에 이제 아장거리며 걷기 시작하는 영유아가 있는 집은 조심, 또 조심.

<끝이 날카로운 키캡. 찔리면 어른이라도 아프다.>

2) 헐렁해지는 키캡

원래 들어있는 키캡도 훌륭하지만, 가끔은 색색의 글쇠로 바꿔보는 재미도 있는 법. 그런데, 이 키보드에 다른 키캡을 꼽으면, 키캡 꼽는 기둥 부위가 헐렁해 진다 – 실제 파란 색 ALT를 꼽아서 썼었는데 어느새 왼쪽 ALT가 헐렁해 졌다. 기둥에 금은 안 가긴 했지만....... 인터넷에 찾아보니 그런 경우가 종종 있는 듯. 결국 이 키보드로 키캡 놀이를 하려면 이 키보드 전용으로 딱 고정시켜야 할 듯.

결론,

체리 기계식 키보드의 그 탱탱거리는 스프링 소리가 듣기 싫은 사람들을 위한 조용한 키보드, 특히 조용한 사무실에서 맘 놓고 두들길 수 있고, 낮은 키캡과 낮은 반발력으로 고속 타이핑에도 정말 좋은 키보드, 사무실용으로 추천.

VIKI(그리고 보니 왜 VIKI라고 불리는지? 상판이 없어서 그렇다면 토플리스(topless)가 맞는 단어 아닌감?)타입을 싫어하는 사람은 절대 피해야 할 키보드, 또한 리얼포스의 그 구분감(Tactile)과 달그락 거리는 키캡 소리를 원하는 사람은 아마, 실망하게 될 것임.

추가적으로, 이 토프레 유사 스위치에 알루미늄을 씌워서 비싸게 파는 제품도 있는 것 같은데, 개인적으로는 비추. 그 가격이면 차라리 리얼포스를 사겠다. 아니, 차라리 아래 그림의 Plum을 사고 남는 돈은 가족과 함께 스테이크를 먹는 선택을 하겠다.

1802년, 케임브리지 대학이 낸 수학문제

오늘은 1802년, 영국의 어느 대학에서 출제한 수학문제를 풀어보자.

보기만 해도 머리가 아파오지만,

1. 일단은 무한수의 합이 얼마인지에 대한 문제.

2. 분모가 1x2, 2x3, 3x4, ... 즉 (n * (n+1)) 식의 패턴을 가지고 있다는 것 까지는 알 수 있을 것 같다.

...

아래 해결방법을 보기 전에, 어떻게 해결해야 할지, 깊게 숨을 한 번 내쉬어 보고, 더불어 아래의 광고도 한 번 보면서, 해결 방법에 대해 조금 생각해 보는 시간을 가져보자.

준비 되었으면,

1. 앞에서 이야기한 바와 같이, 분모가 [n(n + 1)]이므로 식을 단순화 하면, 1/[n(n + 1)]

2. 이 문제의 트릭은 분모가 두개의 조건, n 과 n+1의 곱을 가지고 있다는 것이다. 이것은 (n+1)과 (n)을 가진 두개의 분모의 합으로 표현할 수 있다. (이것을 부분분수분해(Partial fraction decomposition)라고 함) 그래서 1번의 단순화 형식을 아래와 같이 나타낼 수 있다.

1/[n(n + 1)] = A/n + B/(n + 1)

3. 양변에 [n(n + 1)]을 곱하면, 1 = A(n + 1) + B(n)

이것은 다시,

1 = An + A + Bn

1 = A + n(A + B)

n의 값에 관계없이 좌우 값이 일치하기 위해서는 n(A+B)가 0 이 되어야 하고, 이 경우 A는 1이다.

A가 1인 경우 B는 –1, 즉

A = 1

A + B = 0

1 + B = 0

B = -1

이제 A, B의 값을 찾았으니, 위의 2번 식에 대입해 보면,

1/[n(n + 1)] = 1/n – 1/(n + 1)

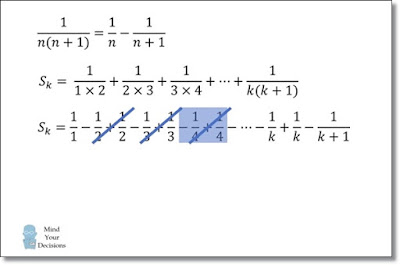
이것을 이용하면 아래와 같이 문제를 더 단순화 할 수 있다.

1/(1×2) = 1/1 – 1/2

1/(2×3) = 1/2 – 1/3

1/(3×4) = 1/3 – 1/4

…

이제 남는 것은,

Sk = 1 – 1/(k + 1)

k가 무한대로 수렴할 때, – 1/(k + 1) = 0

그러므로,

1/(1×2) + 1/(2×3) + 1/(3×4) + … = 1 !!!

학위를 받기 위해 이런 문제를 풀어야 했던 1802년도 케임브리지 대학생들에게 경의를 보낸다.

...

그럼 우리나라는, 1802년 우리나라에는 어떤 일이 있었을까? 궁금했다. 

1802년, 영,정조시대가 끝나고 즉위한 순조. 그 순조2년이 바로 1802년.

안동김씨의 세도정치가 시작된 해. 그로 인해 피폐해진 민심에 1811년, 홍경래의 난이 발생하는 등 이후 60년 동안 외척들로 인해 나라와 백성의 삶이 어려워지기 시작한 원년이 1802년.

서양의 학생들이 고등수학의 해법을 고민하던 때, 우리나라는 왕의 친족이라는 이유만으로 백성의 등골을 빼먹는 자들의 지배가 시작되는 해, 1802년....... 흠.

(알림) 블로그에 올린 글들은 Presh Talwalkar의 유투브 영상과 그의 블로그에서 가져온 것임을 밝힙니다. Presh Talwalkar의 블로그는 여기로 가시면 볼 수 있습니다. 참고로 그의 블로그에는 위 문제가 실린 케임브리지 대학의 출판물 인쇄본 링크외에도 수학과 관련된  좋은 정보도 많이 있습니다. 관심있는 분들은 필히 방문!

제임스 플린 - 왜 우리 세대의 아이큐(IQ)가 이전 세대(grandparent) 보다 높은가?

  재미있다. 영상 내내 단순하지만, 그러나 직설적인 화법은 피하면서도, 20분 내내 결코 말하고자 하는 핵심은 놓치지 않는다. 대단한 할아버지.

  영상 말미쯤 가면 역사와 다른 나라의 상황에 대해 무지한 사람은 정치를 하면 안 된다고 이야기 하는데, 들리기로는 멍청한 사람이 정치인을 해서는 안 된다는 말이라기보다는 정치에 참여(직간접으로)하려면 좀 역사와 세계의 상황에 대해 공부하고 알아보라는 이야기로 들린다 - 자신의 멍청함을 이용하는 교활한 정치인들에게 휘둘리지 말라는 의미로....... 좀 더 상상력을 발휘해 보자면 어쩌면, 진보와 보수도 그런 잣대로 구분될 수도 있겠다는 생각 - 수감되어 있는 전직 대통령에 대해 아직도 무죄를 외치면서 추종하는 사람들을 보면 그런 생각도 든다, 어쩌면 이건 지능의 문제일 수도 있겠다고......
  어쨌든, 이분은 영상의 끝에서, '사람들의 인지능력이 과거와 비교할 때 빠르게 상승곡선을 그리고 있다'고, 그래서 미래는 지금보다 더 좋아질 것이라는 긍정적인 신호를 던지는 것도 잊지 않는다 - 너무 멋진 할아버지.

  동영상에서 스피커로 나온 James Flynn, 이분이 누구인지 찾아보았다.
위키에서는 그를,

James Robert Flynn FRSNZ (born 1934) is a New Zealand intelligence researcher.  ... he is famous for his publications about the continued year-after-year increase of IQ scores throughout the world, which is now referred to as the Flynn effect. ... 

라고 설명한다. (전문 링크는 여기) 직업이 intelligence researcher.... 아 이런 직업도 있구나 - 부럽다.

  이런 분과 함께 수업을 할 수 있는 사람들은 행운아, 다시 부럽다.
  직접 모셔올 수는 없어도 동영상으로는 보여 줄 수 있으니, 그것 만으로도 감지덕지. 우리집 아이들에게도 보여 줘야지.